This article has two audiences:
- The VB.NET programmer who wants to see the Graham Scan implemented in VB.NET with comments in English. (The only example I’ve found on the internet has German comments.)
- GTVx application developers who want to see an implementation of the Graham Scan applied to a geospatial task that may be widely applicable.
Option Explicit On
Option Strict On
Imports System.IO
Public Class Form1
Private Sub StartButton_Click(ByVal sender As System.Object, _
ByVal e As System.EventArgs) _
Handles StartButton.Click
' a mechanism to loop through all the circuits...
For Each circuit As String In circuits
Try
filterId = filterId + 1
' build a list of vertices of the
' conductors for a circuit...
Dim pList As New List(Of Point)
pList = BuildPointList(circuit)
' find the start point (the one with minimal Y)
Dim startPoint As New Point
Dim pCount As Integer = pList.Count - 1
Dim yList(pCount) As Integer
For j As Integer = 0 To pCount
yList(j) = pList(j).Y
Next
Dim minY As Integer = yList.Min
' now find the index of the minimal point...
Dim i As Integer = 0
For i = 0 To pCount
If pList(i).Y = minY Then
startPoint = pList(i)
Exit For
End If
Next
' sort all points by polar coordinate
' against startpoint...
Dim sortedList As List(Of Point) = _
PreSortPoints(pList, startPoint, i)
' do the Graham Scan...
Dim convexList As New List(Of Point)
convexList = GrahamScan(sortedList)
Catch ex As Exception
'Logtime("Error in processing circuit " & circuit)
End Try
Application.DoEvents()
Next
End Sub
Private Function PreSortPoints(ByRef pList As List(Of Point), _
ByVal startPoint As Point, _
ByVal startPointIndex As Integer) _
As List(Of Point)
' start a new list and fill it with the
' start point, then all the points in pList '
' up to the startpoint, then
' all the points after the start point...
Dim sortedList As New List(Of Point)
sortedList.Add(startPoint)
For i As Integer = 0 To startPointIndex - 1
sortedList.Add(pList(i))
Next
For i As Integer = startPointIndex + 1 To pList.Count - 1
sortedList.Add(pList(i))
Next
' then sort the list by angle from zero,
' in preparation for the Graham Scan...
sortedList.Sort(1, sortedList.Count - 1, _
New FunctionComparer(Of Point)(Function(a, b) _
Orientation(sortedList(0), a, b)))
Return sortedList
End Function
' Does the point C lie counterclockwise or
' clockwise of the vector AB?
' If counterclockwise, return a positive number.
' If clockwise, return a negative number.
' If A, B, and C are colinear, return zero.
Private Function Orientation(ByVal A As Point, _
ByVal B As Point, _
ByVal C As Point) As Integer
Dim dif1 As Double = (B.X - A.X)
Dim dif2 As Double = (C.Y - A.Y)
Dim dif3 As Double = (C.X - A.X)
Dim dif4 As Double = (B.Y - A.Y)
Dim tmp As Double = (dif1 * dif2) - (dif3 * dif4)
If tmp < 0 Then
Return 1
ElseIf tmp > 0 Then
Return -1
Else
Return 0
End If
End Function
Private Function GrahamScan(ByVal slist As List(Of Point)) _
As List(Of Point)
Dim convexList As New List(Of Point)
If slist.Count < 4 Then
Return slist
Else
convexList.Add(slist(0))
convexList.Add(slist(1))
For j As Integer = 2 To slist.Count - 1
Do Until (convexList.Count < 2) OrElse _
Orientation(convexList(convexList.Count - 2), _
convexList(convexList.Count - 1), _
slist(j)) < 0
' i.e., if Orientation returns a
' number < 0 then remove the previous point
convexList.RemoveAt(convexList.Count - 1)
Loop
' in either case, add a point from slist...
convexList.Add(slist(j))
Next
Return convexList
End If
End Function
The VB.NET Project in a Zip File
Download here.
Discussion of the code
- The venerable Graham Scan was published in 1972. It builds a Convex Hull (CH) for an arbitrary sets of points in the Cartesian plane. (I have sometimes called the CH a “minimal bounding convex polygon”.) It first finds the coordinate pair with minimal Y. Then sorts the point set by polar coordinate from right to left with respect to the x axis. It then uses an algorithm to pick which of these points will remain in the CH. It runs in NlogN time. That is a terribly brief description, but I direct the reader to the references for further detail and insight.
- I altered the VB.NET code in the function “Orientation” in the German example because an integer value was routinely exceeding its capacity.
- I also altered the comparison function to return a 1, 0, or -1 instead of the actual value of an expression that is positive, zero, or negative depending on the slope of two lines.
- The whole subject of .NET interfaces, IComparable, and IComparer deserves a series of articles that I am not competent to write. I invite the reader to do his own research.
- I did not implement point thinning (interior point elimination). In the Year of Our Lord 2011, most computers are able to do the full Graham Scan of all the points in each circuit (in my case, from 0 to 2791) in a reasonable time. In fact, now would be a good time to share some performance numbers. There are 253 circuits at Huntsville Utilities. In the total of these circuits, there are 85,078 conductors. The GTVx application that reads in a list of circuit names and for each of the 253 circuits uses a query to build a point list of conductor vertices, then sorts the point list, then does the Graham Scan to determine the CH, then places a redline shape element defined by the CH, then finds the streets within the shape, and then writes a text file with each circuit name followed by the street names that fall within its area, takes under 5 minutes to run.
Practical results in GTViewer – What Problem is Solved?
This section is primarily intended for the audience of GTVx application developers.
We get questions from our users. If we are lucky. And if we are very lucky indeed, we get interesting questions. The application above rose from one: “Hey Charlie, is there any way to tell what streets are near a circuit?” “Probably, tell me more.” “Well, the dispatch department keeps a bunch of facts about each circuit. A map. The substation name. More stuff. And a list of the streets that are close to it. They look on a printed map and copy down the street names. Sure would be nice to do automatically.”
One of the most fortunate things that happens to GTVx application developers is that we can ask Joey Rogers how it would be most appropriate to approach a problem. In this case, he pointed me to the Graham Scan and a few web sites that describe it. And scanned a chapter of a textbook about the Graham Scan. From these, I was able to develop the code in the zip file. I think anyone who has worked for more than a few days with GTVx will recognize the techniques used in the project. Almost all of them come directly from code examples in the GTVx documentation.
Here’s a sketch of the approach: It’s pretty straightforward to use a query to get all the primary conductors on a circuit. Then it’s easy to get all their vertices. That is the point set processed by the two-step Graham Scan. Once you have an ordered list of points describing the convex hull, you can use that list to place a redline shape. Then you can count all the street features within the shape and use the CountDetails method to make a list of street names. Then you sort them and place them in a Listbox. Once all the circuits have been processed, you can write the Listbox contents to a text file. Done.
Not perfect. The convex hull surrounding a circuit may contain streets that are not very close to any conductor on that circuit. So the list of streets produced by the application is in practical terms a superset of street names from which inappropriate street names will need to be removed. I suspect this will turn out to be a manual task. But it makes producing the final lists of streets much simpler than starting with a map and a pencil.
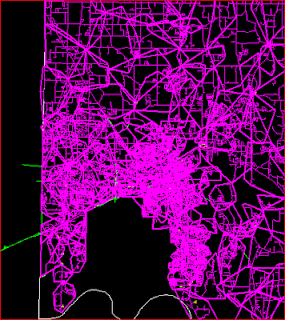
Screen Shots
- The full application form with GTVx control and Listbox for debugging.
- Detail of a single circuit area.
- The GTVx control with all circuits highlighted.
- http://www.iti.fh-flensburg.de/lang/algorithmen/geo/graham.htm - Includes a discussion of the Graham Scan in German, code in C, and a citation of Graham’s original paper in 1972.
- http://www.activevb.de/tipps/vbnettipps/tipp0113.html - Includes code in VB.NET with comments on German.
- http://www.cs.princeton.edu/courses/archive/fall06/cos226/lectures/geometry.pdf - Looks like a PowerPoint presentation lecture on various geometric algorithms, including the Graham Scan, in English.
- http://en.wikipedia.org/wiki/Graham_scan - Good article, in English, includes pseudo-code and some nuances of processing since 1972.
- Robert Sedgewick, Algorithms in C++, 1992. Chapter 25.